1 问题描述
我最近在复现一篇论文的实验:Speech Emotion: Investigating Model Representations, Multi-Task Learning and Knowledge Distillation(Mitra et al. 2022), 这是在MSP-Podcast(Busso et al. 2025)这个语音情感数据集上做Arousal,Valence, Dominace三个维度的回归任务。论文模型结构图如下
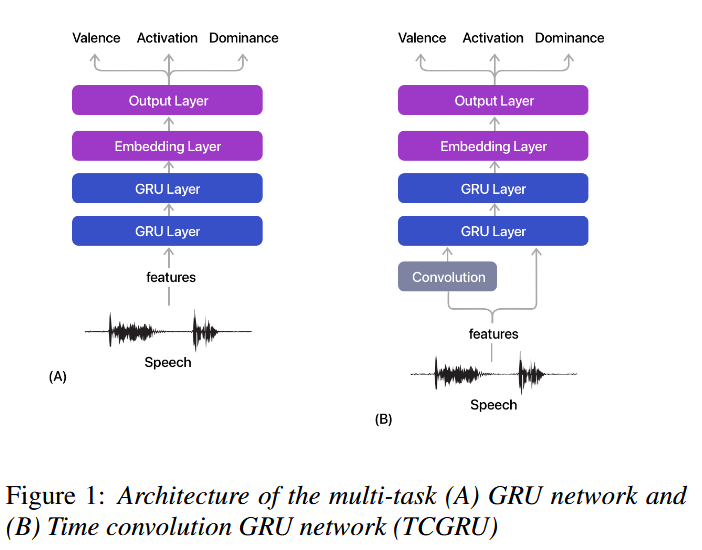
我复现的是左边这个模型,它是先用预训练模型对数据进行特征提取,然后把特征送到 two GRU Layer——Embedding Layer(其实就是Linear Layer)——Linear Layer 这个网络结构里,这个模型用到的损失函数并不是MSE,而是自己定义,公式如下所示
$$ L_{ccc} := 1 - (\alpha CCC_v + \beta CCC_a + (1 - \alpha - \beta) CCC_d) $$
$$ CCC = \frac{2\rho \sigma_x \sigma_y}{\sigma_x^2 + \sigma_y^2 + (\mu_x - \mu_y)^2} $$
其中$\alpha = \beta = \frac{1}{3}$,$\rho$是皮尔逊相关系数,$\sigma_x$、$\sigma_y$分别为变量$x$和$y$的标准差,$\mu_x$、$\mu_y$分别为变量$x$、$y$的均值,$\sigma_x^2和\sigma_y^2$是衡量数据离散程度的指标。这个公式可以拆解为两个关键部分:
A. 分子: $2\rho\sigma_x\sigma_y$ 这个部分与 $x$ 和 $y$ 之间的协方差紧密相关(协方差 = $\rho\sigma_x\sigma_y$)。它主要反映了两个变量的相关性强度。
B. 分母: $\sigma_x^2 + \sigma_y^2 + (\mu_x - \mu_y)^2$ 这是理解 CCC 精髓的地方。它衡量了两个变量之间的差异,由三部分组成:
- $\sigma_x^2$:预测值的离散程度。
- $\sigma_y^2$:真实值的离散程度。
- $(\mu_x - \mu_y)^2$:位置偏移惩罚项。这是 CCC 的核心!如果预测值的均值与真实值的均值不相等(即 $\mu_x \neq \mu_y$),这个惩罚项就会大于0,从而导致分母变大,最终使 CCC 的总分降低。
2 核心思想:从"相关"到"一致"
要理解CCC,首先要明白它与更常见的皮尔逊相关系数(Pearson’s Correlation Coefficient, 符号为$\rho$)的区别
- 皮尔逊相关系数($\rho$):衡量的是两个变量之间的线性相关性。它关心当一个变量增加时,另一个变量是否也倾向于以线性的方式增加(正相关)或减少(负相关)。它不关心两个变量的绝对数值是否相等。
- 一致性相关系数(CCC):衡量的则是两个变量之间的一致性或吻合度(Agreement)。它不仅要求两个变量有很强的线性关系,还要求他们的数值本身非常接近。
2.1 示例场景
我们通过一个具体的例子,一步步手动计算皮尔逊相关系数 ($\rho$) 和一致性相关系数 (CCC),来清晰地展示它们之间的核心区别。
假设有一个模型,其任务是预测一个范围在1-10的数值。我们有一组包含5个数据点的真实值和模型预测值。
- 真实值 (Y):
[1, 2, 3, 4, 5] - 模型预测值 (X):
[3, 4, 5, 6, 7]
直观来看,这个模型的预测趋势是完美的,当真实值增加1时,预测值也恰好增加1。但是,它的预测值存在一个系统性偏差,即总是比真实值高2。
现在,我们来计算两个指标,看看它们如何评价这个模型。
1. 皮尔逊相关系数 ($\rho$) 的计算
公式: $$\rho = \frac{\sum_{i=1}^{n}(x_i - \mu_x)(y_i - \mu_y)}{\sqrt{\sum_{i=1}^{n}(x_i - \mu_x)^2 \sum_{i=1}^{n}(y_i - \mu_y)^2}}$$
计算步骤:
第一步:计算均值 (μ)
- 真实值均值: $\mu_y = (1+2+3+4+5) / 5 = 3$
- 预测值均值: $\mu_x = (3+4+5+6+7) / 5 = 5$
第二步:计算每个数据点与均值的偏差
| $y_i$ | $y_i - \mu_y$ | $x_i$ | $x_i - \mu_x$ |
|---|---|---|---|
| 1 | -2 | 3 | -2 |
| 2 | -1 | 4 | -1 |
| 3 | 0 | 5 | 0 |
| 4 | 1 | 6 | 1 |
| 5 | 2 | 7 | 2 |
第三步:计算公式的分子 (协方差部分) 将两列偏差相乘并求和: $\sum(x_i - \mu_x)(y_i - \mu_y) = (-2 \times -2) + (-1 \times -1) + (0 \times 0) + (1 \times 1) + (2 \times 2) $$ = 4 + 1 + 0 + 1 + 4 = 10 $
第四步:计算公式的分母 (标准差部分)
计算Y的离差平方和: $\sum(y_i - \mu_y)^2 = (-2)^2 + (-1)^2 + 0^2 + 1^2 + 2^2 = 4+1+0+1+4 = 10$
计算X的离差平方和: $\sum(x_i - \mu_x)^2 = (-2)^2 + (-1)^2 + 0^2 + 1^2 + 2^2 = 4+1+0+1+4 = 10$
分母为: $\sqrt{10 \times 10} = \sqrt{100} = 10$
第五步:计算最终的 $\rho$ $$\rho = \frac{10}{10} = 1.0$$
结论:皮尔逊相关系数为1.0,表示模型的预测与真实值之间存在完美的线性关系。
2. 一致性相关系数 (CCC) 的计算
公式: $$CCC = \frac{2\rho\sigma_x\sigma_y}{\sigma_x^2 + \sigma_y^2 + (\mu_x - \mu_y)^2}$$
计算步骤:
第一步:准备所需组件
- 从上面的计算中,我们已知:
- $\rho = 1.0$
- $\mu_y = 3$
- $\mu_x = 5$
- 我们还需要计算方差 ($\sigma^2$) 和标准差 ($\sigma$)。
第二步:计算方差 ($\sigma^2$) 方差是离差平方和的平均值。
- 真实值方差: $\sigma_y^2 = \frac{\sum(y_i - \mu_y)^2}{n} = \frac{10}{5} = 2$
- 预测值方差: $\sigma_x^2 = \frac{\sum(x_i - \mu_x)^2}{n} = \frac{10}{5} = 2$
第三步:计算标准差 ($\sigma$)
$\sigma_y = \sqrt{2} \approx 1.414$
$\sigma_x = \sqrt{2} \approx 1.414$
第四步:计算CCC公式的分子 $2 \rho \sigma_x \sigma_y = 2 \times 1.0 \times \sqrt{2} \times \sqrt{2} = 2 \times 2 = 4$
第五步:计算CCC公式的分母 这是最关键的一步,它包含了惩罚项。 $\sigma_x^2 + \sigma_y^2 + (\mu_x - \mu_y)^2 $$ = 2 + 2 + (5 - 3)^2 $ $= 4 + (2)^2 $$ = 4 + 4 = 8 $
第六步:计算最终的 CCC $$CCC = \frac{4}{8} = 0.5$$
结论:一致性相关系数为0.5,表示模型的预测与真实值之间一致性中等。
这个例子清晰地表明,当评估一个需要产出精确数值的回归模型时,皮尔逊相关系数可能会给出具有误导性的、过于乐观的评价。而 CCC 则提供了一个更真实、更可靠的性能度量,因为它同时考虑了趋势(相关性)和数值的吻合度(一致性)。
3. 如何解读CCC的值?
CCC 的取值范围是 -1 到 +1:
- +1:表示完美一致。预测值与真实值完全相等。
- 0:表示完全不一致或没有关系。
- -1:表示完美不一致(例如,预测值与真实值呈完美的相反线性关系)。